With the huge payloads of data everywhere, Statistics has emerged as one of the key pre-requisite for engineers who want to become the expert in machine learning. Statistical Techniques are useful in making many crucial decisions that impact our lives and help you to make professional decisions that involve data. Knowledge of statistical methods make a huge contribution in effective decision making. So, we will learn some basics around Statistics and its terminology during the course of this article.
Terminologies in Statistics
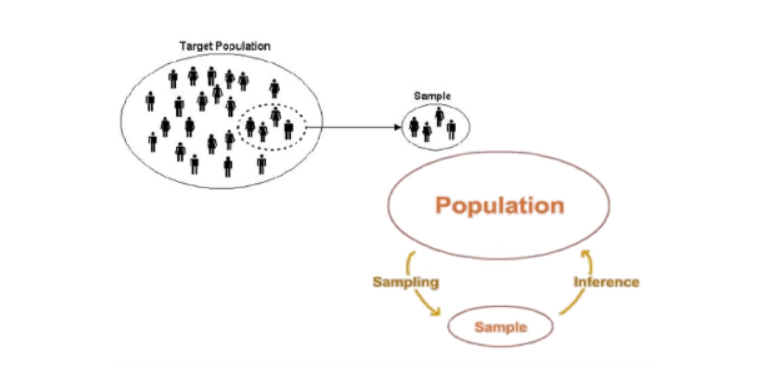
Four big terms in statistics are population, sample, parameter, and statistic.
- Population: A population is the entire group of individuals
- Sample: A data sample is a set of data collected and/or selected from a statistical population by a defined procedure. The elements of a sample are known as sample points, sampling units or observations. The sample usually represents a subset of manageable size.
- Parameter: A parameter is something in an equation that is passed on in an equation
- Statistic: A statistic is a quantitative characteristic of a sample that often helps estimate or test the population parameter (such as a sample mean or proportion).
Population
In statistics, the term population is used to describe the subjects of a particular study—everything or everyone who is the subject of a statistical observation.
Populations can be large or small in size and defined by any number of characteristics, though these groups are typically defined specifically rather than vaguely—for instance, a population of women over 18 who buy coffee at Starbucks rather than a population of women over 18. Statistical populations are used to observe behaviors, trends, and patterns in the way individuals in a defined group interact with the world around them, allowing statisticians to draw conclusions about the characteristics of the subjects of study, although these subjects are most often humans, animals, and plants, and even objects like stars.
Data Sample
In statistics and quantitative research methodology, a data sample is a set of data collected and/or selected from a statistical population by a defined procedure. This refers to a set of actual measurements. The distinction between sample and population statistics is most important for a small number of measurements (less than 20).The elements of a sample are known as sample points, sampling units or observations. The sample usually represents a subset of manageable size. Different sampling techniques, such as forming stratified samples, can help in dealing with subpopulations, and many of these techniques assume that a specific type of sample, called a simple random sample, has been selected from the population.
Statistical Investigation
Statistical investigation is part of an information gathering and learning process which is undertaken to seek meaning from and to learn more about observed phenomena as well as to inform decisions and actions. The ultimate goal of statistical investigation is to learn more about a real world situation and to expand the body of contextual knowledge. Sampling In statistics, quality assurance, and survey methodology, sampling is the selection of a subset (a statistical sample) of individuals from within a statistical population to estimate characteristics of the whole population. Two advantages of sampling are that the cost is lower and data collection is faster than measuring the entire population. Representative Sample A representative sample is a small quantity of something that accurately reflects the larger entity. An example is when a small number of people accurately reflect the members of an entire population.
Sampling
In statistics, quality assurance, and survey methodology, sampling is the selection of a subset (a statistical sample) of individuals from within a statistical population to estimate characteristics of the whole population. Two advantages of sampling are that the cost is lower and data collection is faster than measuring the entire population.
Representative Sample
A representative sample is a small quantity of something that accurately reflects the larger entity. An example is when a small number of people accurately reflect the members of an entire population.
Bias
Statistical bias is a feature of a statistical technique or of its results whereby the expected value of the results differs from the true underlying quantitative parameter being estimated.
Sampling Bias
In statistics, sampling bias is a bias in which a sample is collected in such a way that some members of the intended population are less likely to be included than others. It results in a biased sample, a non-random sample of a population (or non-human factors) in which all individuals, or instances, were not equally likely to have been selected. If this is not accounted for, results can be erroneously attributed to the phenomenon under study rather than to the method of sampling.
Types Of Sampling Methods
Simple Random Sampling (SRS)
- In a simple random sample (SRS) of a given size, all such subsets of the frame are given an equal probability.
- Each element of the frame thus has an equal probability of selection: the frame is not subdivided partitioned.
- Any given pair of elements has the same chance of selection as any other such pair (and similarly for triples, and so on). This minimizes bias and simplifies analysis of results.
- In particular, the variance between individual results within the sample is a good indicator of variance in the overall population, which makes it relatively easy to estimate the accuracy of results.
- SRS can be vulnerable to sampling error because the randomness of the selection may result in a sample that doesn’t reflect the makeup of the population.
Stratified Sampling
It is possible when it makes sense to partition the population into groups based on a factor that may influence the variable that is being measured. These groups are then called strata. An individual group is called a stratum. With stratified sampling one should:
- partition the population into groups (strata)
- obtain a simple random sample from each group (stratum)
- collect data on each sampling unit that was randomly sampled from each group (stratum)
Cluster Sampling
It is very different from Stratified Sampling. With cluster sampling one should
- divide the population into groups (clusters).
- obtain a simple random sample of so many clusters from all possible clusters.
- obtain data on every sampling unit in each of the randomly selected clusters.
Systematic Sampling
- Systematic sampling (also known as interval sampling) relies on arranging the study population according to some ordering scheme and then selecting elements at regular intervals through that ordered list.
- Systematic sampling involves a random start and then proceeds with the selection of every kth element from then onwards.
- It is easy to implement and the stratification induced can make it
- However, systematic sampling is especially vulnerable to periodicities in the list. If periodicity is present and the period is a multiple or factor of the interval used, the sample is especially likely to be unrepresentative of the overall population, making the scheme less accurate than simple random sampling.
- Systematic sampling is that even in scenarios where it is more accurate than SRS, its theoretical properties make it difficult to quantify that accuracy.
Quantitative and Qualitative data
Quantitative and qualitative data provide different outcomes, and are often used together to get a full picture of a population. For example, if data are collected on annual income (quantitative), occupation data (qualitative) could also be gathered to get more detail on the average annual income for each type of occupation. Quantitative and qualitative data can be gathered from the same data unit depending on whether the variable of interest is numerical or categorical.
Quantitative data
Information that can be handled numerically. Quantitative variables are numerical variables: counts, percents, or numbers.
- Quantitative data always are associated with a scale measure.
- Probably the most common scale type is the ratio-scale. Observations of this type are on a scale that has a meaningful zero value but also have an equidistant measure
- Statistics that describe or summarize can be produced for quantitative data and to a lesser extent for qualitative data.
- As quantitative data are always numeric they can be ordered, added together, and the frequency of an observation can be counted. Therefore, all descriptive statistics can be calculated using quantitative data.
- By making inferences about quantitative data from a sample, estimates or projections for the total population can be produced.
- Quantitative data can be used to inform broader understandings of a population
Qualitative data
Qualitative data Information that refers to the quality of something. Ethnographic research, participant observation, open-ended interviews, etc., may collect qualitative data. However, often there is some element of the results obtained via qualitative research that can be handled numerically, e.g., how many observations, number of interviews conducted, etc.
- Qualitative data are measures of ‘types’ and may be represented by a name, symbol, or a number code.
- Qualitative data are data about categorical variables (e.g. what type).
- Statistics that describe or summarize can be produced for quantitative data and to a lesser extent for qualitative data.
- As qualitative data represent individual (mutually exclusive) categories, the descriptive statistics that can be calculated are limited, as many of these techniques require numeric values which can be logically ordered from lowest to highest and which express a count.
- Qualitative data are not compatible with inferential statistics as all techniques are based on numeric values.
- It is used to consider how a population may change or progress into the future.is Qualitative data
- Descriptive Statistics
Types of Statistics
Descriptive Statistics
Descriptive statistics give information that describes the data in some manner. For example, suppose a pet shop sells cats, dogs, birds and fish. If 100 pets are sold, and 40 out of the 100 were dogs, then one description of the data on the pets sold would be that 40% were dogs.This same pet shop may conduct a study on the number of fish sold each day for one month and determine that an average of 10 fish were sold each day. The average is an example of descriptive statistics.Some other measurements in descriptive statistics answer questions such as ‘How widely dispersed is this data?’, ‘Are there a lot of different values?’ or ‘Are many of the values the same?’, ‘What value is in the middle of this data?’, ‘Where does a particular data value stand with respect with the other values in the data set?’
A graphical representation of data is another method of descriptive statistics. Examples of this visual representation are histograms, bar graphs and pie graphs, to name a few. Using these methods, the data is described by compiling it into a graph, table or other visual representation. This provides a quick method to make comparisons between different data sets and to spot the smallest and largest values and trends or changes over a period of time. If the pet shop owner wanted to know what type of pet was purchased most in the summer, a graph might be a good medium to compare the number of each type of pet sold and the months of the year.
Inferential statistics
Inferential statistics is one of the two main branches of statistics. Inferential statistics use a random sample of data taken from a population to describe and make inferences about the population. For instance, we use inferential statistics to try to infer from the sample data what the population might think. Or, we use inferential statistics to make judgments of the probability that an observed difference between groups is a dependable one or one that might have happened by chance in this study. Thus, we use inferential statistics to make inferences from our data to more general conditions; we use descriptive statistics simply to describe what’s going on in our data.
Properties of samples, such as the mean or standard deviation, are not called parameters, but statistics. Inferential statistics are techniques that allow us to use these samples to make generalizations about the populations from which the samples were drawn. It is, therefore, important that the sample accurately represents the population. The process of achieving this is called sampling (sampling strategies are discussed in detail here on our sister site). Inferential statistics arise out of the fact that sampling naturally incurs sampling error and thus a sample is not expected to perfectly represent the population. The methods of inferential statistics are (1) the estimation of parameter(s) and (2) testing of statistical hypotheses.
Random Variable
In probability and statistics, a random variable, random quantity, aleatory variable, or stochastic variable is a variable whose possible values are outcomes of a random phenomenon. As a function, a random variable is required to be measurable, which rules out certain cases where the quantity which the random variable returns is infinitely sensitive to small changes in the outcome.
It is common that these outcomes depend on some physical variables that are not well understood. For example, when tossing a fair coin, the final outcome of heads or tails depends on the uncertain physics. Which outcome will be observed is not certain. The coin could get caught in a crack in the floor, but such a possibility is excluded from consideration. The domain of a random variable is the set of possible outcomes. In the case of the coin, there are only two possible outcomes, namely heads or tails. Since one of these outcomes must occur, either the event that the coin lands heads or the event that the coin lands tails must have non-zero probability.
A random variable is defined as a function that maps the outcomes of unpredictable processes to numerical quantities (labels), typically real numbers. In this sense, it is a procedure for assigning a numerical quantity to each physical outcome. Contrary to its name, this procedure itself is neither random nor variable. Rather, the underlying process providing the input to this procedure yields random (possibly non-numerical) output that the procedure maps to a real-numbered value.
Discrete random variable
In an experiment a person may be chosen at random, and one random variable may be the person’s height. Mathematically, the random variable is interpreted as a function which maps the person to the person’s height. Associated with the random variable is a probability distribution that allows the computation of the probability that the height is in any subset of possible values, such as the probability that the height is between 180 and 190 cm, or the probability that the height is either less than 150 or more than 200 cm.
Continuous random variable
A variable is a quantity that has a changing value; the value can vary from one example to the next. A continuous variable is a variable that has an infinite number of possible values. In other words, any value is possible for the variable.An example of a continuous random variable would be one based on a spinner that can choose a horizontal direction. Then the values taken by the random variable are directions. We could represent these directions by North, West, East, South, Southeast, etc.
Some examples of continuous variables:
- Time
- A person’s weight.
- Income.
- Age.
- The price of gas.
Discrete Variable
A variable is a quantity that has changing values. A discrete variable is a variable that can only take on a certain number of values. In other words, they don’t have an infinite number of values. If you can count a set of items, then it’s a discrete variable. The opposite of a discrete variable is a continuous variable. Continuous variables can take on an infinite number of possibilities.
Some examples of discrete variables:
- Number of quarters in a purse, jar, or bank
- The number of cars in a parking lot
- Points on a 10-point rating scale
- Ages on birthday cards.
Key Aspects of Random Variable
Distribution
Suppose a variable X can take the values 1, 2, 3, or 4. … It is a function giving the probability that the random variable X is less than or equal to x, for every value x. For a discrete random variable, the distribution function is found by summing up the probabilities.
Mean
The mean of a discrete random variable X is a weighted average of the possible values that the random variable can take. Unlike the sample mean of a group of observations, which gives each observation equal weight, the mean of a random variable weights each outcome xi according to its probability, pi.
Standard Deviation
The standard deviation is a measure of the spread of scores within a set of data. Usually, we are interested in the standard deviation of a population. However, as we are often presented with data from a sample only, we can estimate the population standard deviation from a sample standard deviation. These two standard deviations – sample and population standard deviations – are calculated differently. In statistics, we are usually presented with having to calculate sample standard deviations, and so this is what this article will focus on, although the formula for a population standard deviation will also be shown.
The sample standard deviation formula is:

Z Score
A z-score (aka, a standard score) indicates how many standard deviations an element is from the mean. A z-score can be calculated from the following formula.
z = (X – μ) / σ
where z is the z-score, X is the value of the element, μ is the population mean, and σ is the standard deviation.

How to interpret z-scores
- A z-score less than 0 represents an element less than the mean.
- A z-score greater than 0 represents an element greater than the mean.
- A z-score equal to 0 represents an element equal to the mean.
- A z-score equal to 1 represents an element that is 1 standard deviation greater than the mean; a z-score equal to 2, 2 standard deviations greater than the mean; etc.
- A z-score equal to -1 represents an element that is 1 standard deviation less than the mean; a z-score equal to -2, 2 standard deviations less than the mean; etc.
- If the number of elements in the set is large, about 68% of the elements have a z-score between -1 and 1; about 95% have a z-score between -2 and 2; and about 99% have a z-score between -3 and 3.






