The perceptron is the basic unit powering what is today known as deep learning. It is the artificial neuron that, when put together with many others like it, can solve complex, undefined problems much like humans do. Understanding the mechanics of the perceptron (working on its own) and multilayer perceptrons (working together) will give you an important foundation for understanding and working with modern neural networks.
What Is a Perceptron?
A perceptron is a simple binary classification algorithm, proposed by Cornell scientist Frank Rosenblatt. It helps to divide a set of input signals into two parts—“yes” and “no”. But unlike many other classification algorithms, the perceptron was modeled after the essential unit of the human brain—the neuron and has an uncanny ability to learn and solve complex problems.
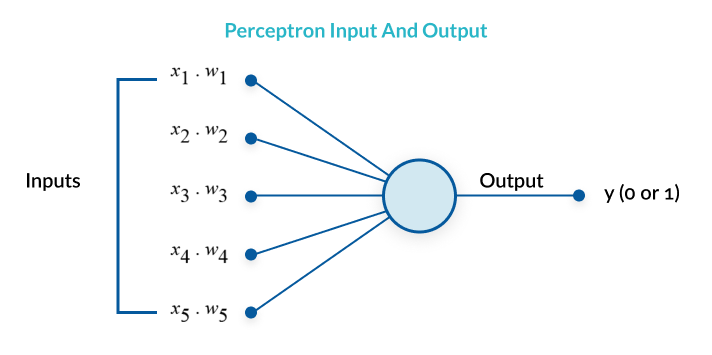
A perceptron is a very simple learning machine. It can take in a few inputs, each of which has a weight to signify how important it is, and generate an output decision of “0” or “1”. However, when combined with many other perceptrons, it forms an artificial neural network. A neural network can, theoretically, answer any question, given enough training data and computing power.
What Is a Multilayer Perceptron?
A multilayer perceptron (MLP) is a perceptron that teams up with additional perceptrons, stacked in several layers, to solve complex problems. The diagram below shows an MLP with three layers. Each perceptron in the first layer on the left (the input layer), sends outputs to all the perceptrons in the second layer (the hidden layer), and all perceptrons in the second layer send outputs to the final layer on the right (the output layer).
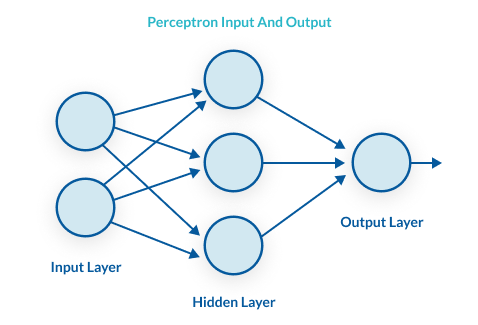
Each perceptron sends multiple signals, one signal going to each perceptron in the next layer. For each signal, the perceptron uses different weights. In the diagram above, every line going from a perceptron in one layer to the next layer represents a different output. Each layer can have a large number of perceptrons, and there can be multiple layers, so the multilayer perceptron can quickly become a very complex system. The multilayer perceptron has another, more common name—a neural network. A three-layer MLP, like the diagram above, is called a Non-Deep or Shallow Neural Network. An MLP with four or more layers is called a Deep Neural Network. One difference between an MLP and a neural network is that in the classic perceptron, the decision function is a step function and the output is binary. In neural networks that evolved from MLPs, other activation functions can be used which result in outputs of real values, usually between 0 and 1 or between -1 and 1. This allows for probability-based predictions or classification of items into multiple labels.
Structure of a Perceptron
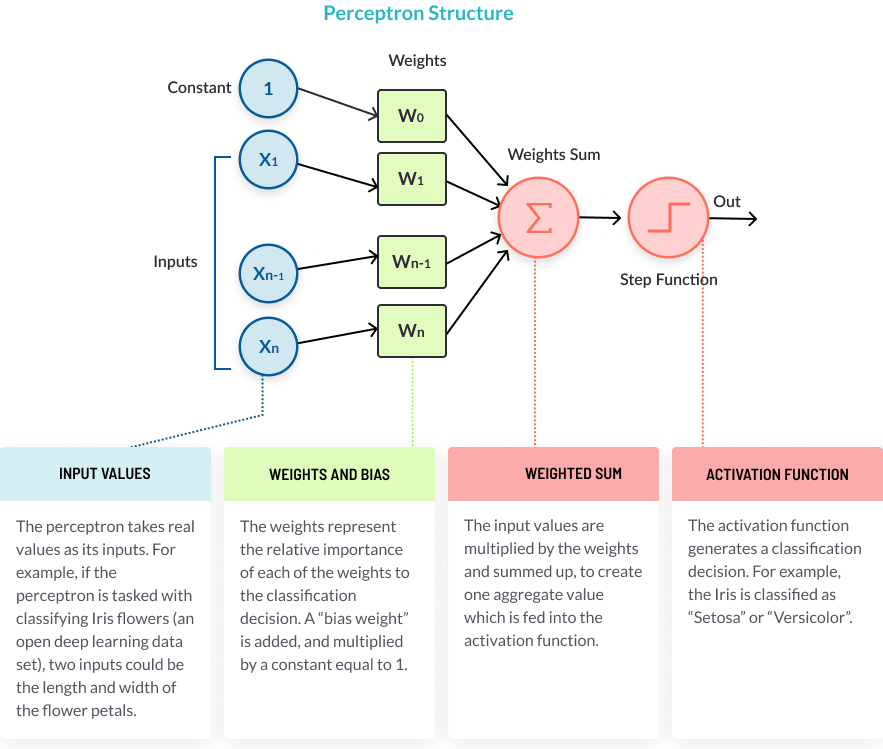
The perceptron, or neuron in a neural network, has a simple but ingenious structure. It consists of four parts, illustrated below.
The Perceptron Learning Process
A perceptron follows these steps:
1. Takes the inputs, multiplies them by their weights, and computes their sum Why It’s Important The weights allow the perceptron to evaluate the relative importance of each of the outputs. Neural network algorithms learn by discovering better and better weights that result in a more accurate prediction. There are several algorithms used to fine tune the weights, the most common is called backpropagation.
2. Adds a bias factor, the number 1 multiplied by a weight Why It’s Important This is a technical step that makes it possible to move the activation function curve up and down, or left and right on the number graph. It makes it possible to fine-tune the numeric output of the perceptron. For more details see our guide on neural network bias.
3. Feeds the sum through the activation function Why It’s Important The activation function maps the input values to the required output values. For example, input values could be between 1 and 100, and outputs can be 0 or 1. The activation function also helps the perceptron to learn, when it is part of a multilayer perceptron (MLP). Certain properties of the activation function, especially its non-linear nature, make it possible to train complex neural networks. For more details see our guide on activation functions.
4. The result is the perceptron output The perceptron output is a classification decision. In a multilayer perceptron, the output of one layer’s perceptrons is the input of the next layer. The output of the final perceptrons, in the “output layer”, is the final prediction of the perceptron learning model.
From the Classic Perceptron to a Full-Fledged Deep Neural Network
Although multilayer perceptrons (MLP) and neural networks are essentially the same thing, you need to add a few ingredients before an MLP becomes a full neural network. These are:
Backpropagation—the backpropagation algorithm allows you to perform a “backward pass”, which helps tune the weights of the inputs. Backpropagation performs iterative backward passes which attempt to minimize the “loss”, or the difference between the known correct prediction and the actual model prediction. With each backward pass, the weights move towards an optimum that minimizes the loss function and results in the most accurate prediction.
Hyperparameters—in a modern neural network, aspects of the multilayer structure such as the number of layers, initial weights, the type of activation function, and details of the learning process, are treated as parameters and tuned to improve the performance of the neural network. Tuning hyperparameters is an art, and can have a huge impact on the performance of a neural network.
Advanced structures—many neural networks use a complex structure that builds on the multilayer perceptron. For example, a Recurrent Neural Network (RNN) uses two neural networks in parallel—one runs the training data from beginning to end, the other from the end to the beginning, which helps with language processing. A Convolutional Neural Network (CNN) uses a three-dimensional MLP—essentially, three multilayer perceptron structures that learn the same data point. This is useful for color images which have three layers of “depth”—red, green and blue.






