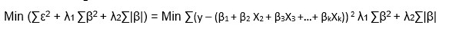Regression models have been around for many years and have proven very useful in modeling real world problems and providing useful predictions, both in scientific and in industry and business environments. In parallel, neural networks and deep learning are growing in adoption, and are able to model complex problems and provide predictions that resemble the learning process of the human brain. What’s the connection between neural networks and regression problems? Can you use a neural network to run a regression? Is there any benefit to doing so?
The short answer is yes—because most regression models will not perfectly fit the data at hand. If you need a more complex model, applying a neural network to the problem can provide much more prediction power compared to a traditional regression.
What is Regression Analysis?
Regression analysis can help you model the relationship between a dependent variable (which you are trying to predict) and one or more independent variables (the input of the model). Regression analysis can show if there is a significant relationship between the independent variables and the dependent variable, and the strength of the impact—when the independent variables move, by how much you can expect the dependent variable to move. The simplest, linear regression equation looks like this:
- y → dependent variable—the value the regression model is aiming to predict
- X2,3..k → independent variables—one or more values that the model takes as an input, using them to predict the dependent variables
- [beta]1,2,3..k → Coefficients—these are weights that define how important each of the variables is for predicting the dependent variable
- [error] → Error—the distance between the value predicted by the model and the actual dependent variable y. Statistical methods can be used to estimate and reduce the size of the error term, to improve the predictive power of the model.
Types of Regression Analysis
Linear Regression
Suitable for dependent variables which are continuous and can be fitted with a linear function (straight line).
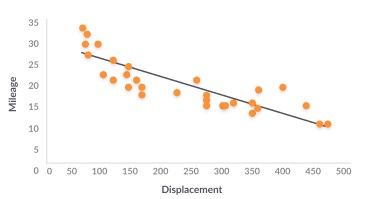
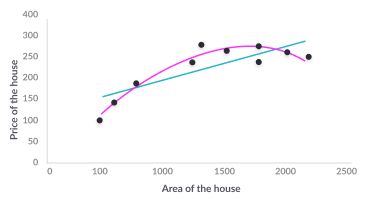
Polynomial Regression
Suitable for dependent variables which are best fitted by a curve or a series of curves. Polynomial models are prone to overfitting, so it is important to remove outliers which can distort the prediction curve.
Logistic Regression
Suitable for dependent variables which are binary. Binary variables are not normally distributed—they follow a binomial distribution, and cannot be fitted with a linear regression function.

Stepwise Regression
An automated regression technique that can deal with high dimensionality—a large number of independent variables. Stepwise regression observes statistical values to detect which variables are significant, and drops or adds co-variates one by one to see which combination of variables maximizes prediction power.

Ridge Regression
A regression technique that can help with multicollinearity—independent variables that are highly correlated, making variances large and causing a large deviation in the predicted value. Ridge regression adds a bias to the regression estimate, reducing or “penalizing’ the coefficients using a shrinkage parameter. Ridge regression shrinks coefficients using least squares, meaning that the coefficients cannot reach zero. Ridge regression is a form of regularization—it uses L2 regularization
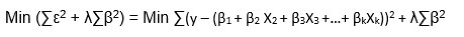
Lasso Regression
Least Absolute Shrinkage and Selection Operator (LASSO) regression, similar to ridge regression, shrinks the regression coefficients to solve the multicollinearity problem. However, Lasso regression shrinks the absolute values, not the least squares, meaning some of the coefficients can become zero. This leads to “feature selection”—if a group of dependent variables are highly correlated, it picks one and shrinks the others to zero. Lasso regression is also a type of regularization—it uses L1 regularization.
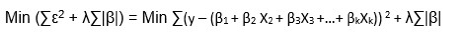
ElasticNet Regression
ElasticNet combines Ridge and Lasso regression, and is trained successively with L1 and L2 regularization, thus trading-off between the two techniques. The advantage is that ElasticNet gains the stability of Ridge regression while allowing feature selection like Lasso. Whereas Lasso will pick only one variable of a group of correlated variables, ElasticNet encourages a group effect and may pick more than one correlated variables.