A Graph Neural Network, also known as a Graph Convolutional Network (GCN), is an image classification method. In this article, we’ll provide an introduction to the concepts of graphs, convolutional neural networks, and Graph Neural Networks. Read on to discover an example of a simple GCN in action, and see applications of graph convolutional networks including, generating predictions in physical systems and image classification.
Graph and Convolutional Neural Network Concepts
Let’s start with basic definitions to get an orientation of the subject.
A graph in computer science is a data structure consisting of Vertices (also called nodes) and Edges (also called connections). Graphs are extremely useful and expressive mathematical structures, which can be used to model real-world phenomena like social networks, molecular structures, semantic structures, geographical or physical models, and more.
Here are two ways to represent a graph: using an equation with a group of vertices V and a group of edges E. And a diagram with nodes and the connections between those nodes. The example below shows a directed graph, but edges can also be undirected.
A Convolutional Neural Network (CNN) is a neural network structure which breaks down an input, typically an image, into smaller pieces and performs feature extraction – it derives important parts of the input which can be used to make a decision, typically a classification decision.
The CNN alternates between convolution and pooling layers. The convolution layers pass a filter over the source image and extract the important information from each piece. The pooling layers take the extracted information and downsample it to retain only the most important information. When the essential data is extracted, it is passed through a fully connected layer to arrive at the final classification decision.
What is Graph Neural Network?
A Graph Neural Network, also known as a Graph Convolutional Networks (GCN), performs a convolution on a graph, instead of on an image composed of pixels. Just like a CNN aims to extract the most important information from the image to classify the image, a GCN passes a filter over the graph, looking for essential vertices and edges that can help classify nodes within the graph.
Extensions of Graph Convolutional Networks
A few important evolutions of GSNs provide additional capabilities:
Attention mechanisms—attention-based Graph Convolutional Networks maintain state information to capture the neighborhood properties of the nodes. This makes it possible to “remember” important nodes and give them higher weights throughout the learning process.
Graph Spatial-Temporal Networks—these are GCNs that can support graphs with a fixed structure but inputs that change over time. For example, a traffic system with a fixed set of roads but a variable traffic arriving over time. Below is one approach to Spatial-Temporal Networks, in which a 1-dimensional CNN layer moves over the X axis, representing time, while the GCN processes the spatial information at each time step.
Graph Generative Networks—can generate new, realistic structures from data, similar to a Generative Adversarial Network. For example, MolGAN is a graph generative architecture that tries to propose a fake molecular graph, while the discriminator aims to distinguish fake graphs from real molecular graphs taken from empirical data. An external evaluation and reward system helps the network generate progressively more realistic graphs.
Example of a Simple GCN Architecture
Below we can see a simple GCN in action. It goes through the following stages:
Normalizing the graph structure and creating an input to the neural network, with node properties and weights.
Graph convolution layer that passes a filter over the nodes and extracts essential features.
Leaky ReLU and dropout layers that perform a sort of pooling/downsampling over the first convolution.
Note: There are new approaches for pooling over a graph representation, which are more elegant and could enable multiple convolutions for GNNs.
Second graph convolution performed on the downsampled graph information.
Softmax layer to perform the final classification decision.
Applications of Graph Convolutional Networks
Generating Predictions in Physical Systems
GCNs can be used to model real-world entities as graphs, and predict their interaction and future behavior. The network can treat real-world objects as vertices, and their interactions as edges. A GCN can make accurate inferences about properties of a physical system, such as collision dynamics, trajectories of objects, and even the effect of objects not seen in the image on other objects.
Image Classification
Image classification was traditionally performed by regular CNNs. However, practitioners are now applying GCN architectures to image classification problems, with encouraging results. A particular focus is on Zero Shot Learning (ZSL), in which a model needs to recognize and label an image belonging to an unknown label, by inferring which known labels it may be similar to. GCNs can use knowledge graphs to categorize a “zero shot”, based on similarities between the images, objects extracted from the images, or semantic information in the category labels.
Community Prediction Using Semi-Supervised Learning
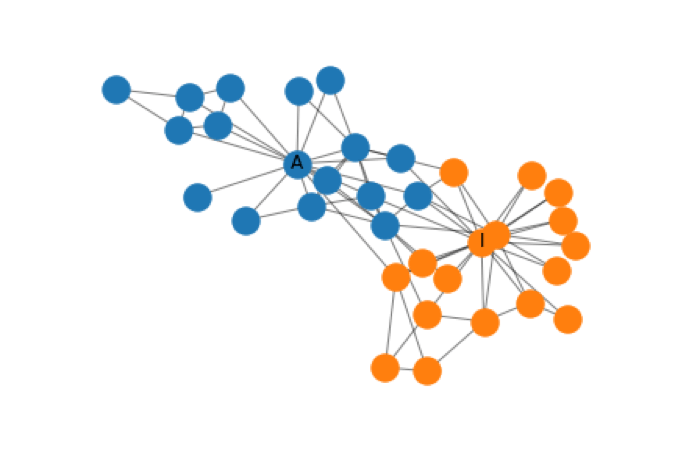
GCNs are used to solve community prediction problems like Zachary’s Karate Club—a small social network where there is a conflict between the administrator and instructor in a karate club, and we need to predict which side each member of the club will choose. A GCN can address similar problems using semi-supervised classification via spectral graph convolutions.
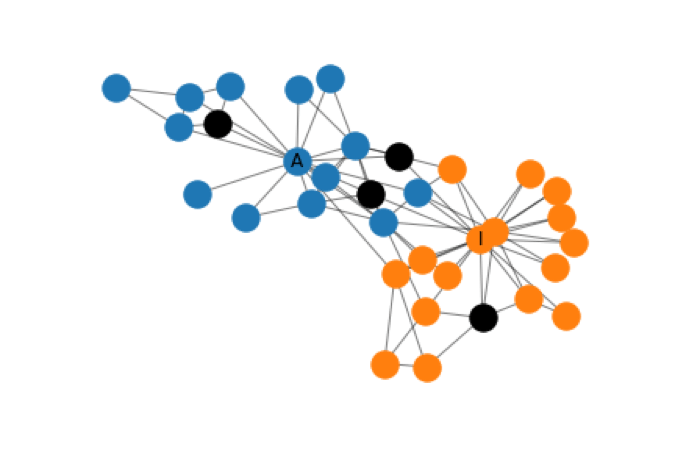
With just using two labeled nodes, a GCN can achieve a high degree of separation and generate accurate predictions for the two communities in the Karate Club problem. Below is the correct Karate Club classification and one of the results obtained by his GCN model.
Correct Classification of Karate Club Problem
Classification Achieved by Jepsen’s GCN Model
Molecular Structure Analysis
Molecular structures are also graph structures. GCNs can learn about existing molecular structures and help researchers discover new ones. Taking a fixed-length molecular fingerprint as their input, they train on known molecules and generate predictions regarding unknown molecular structures. Generative Graph Networks such as MolGAN can be trained to create new molecular structures that have certain desired properties.
Operations Research and Combinatorial Optimization
The field of operations research has a deep interest in combinatorial optimization problems, in which the objective is to find an optimal solution object from a set of objects representing possible strategies. For example, researchers have applied GCNs to the classic travelling salesman problem, combining a GCN with reinforcement learning to iteratively lean a solution, starting from an input graph. GCN outperforms traditional algorithms like Quadratic Assignment Problem.






