Convolution layers in Convolutional Neural Network

Overview

Deep Learning is defined as part of a broader family of machine learning methods based on artificial neural networks with representation learning. Within Deep Learning, there are various terms that are frequently used to explain the Deep Learning Architecture. Let us understand the meaning of Convolution layers in CNN

Convolution Layer

A convolution is defined as the simple application of a filter or a kernel to an input image which reduces the number of features of the image by applying kernel and still keeps its important features which defines the image intact.

The final target of convolution is to identify all important features of the image by keeping minimum features

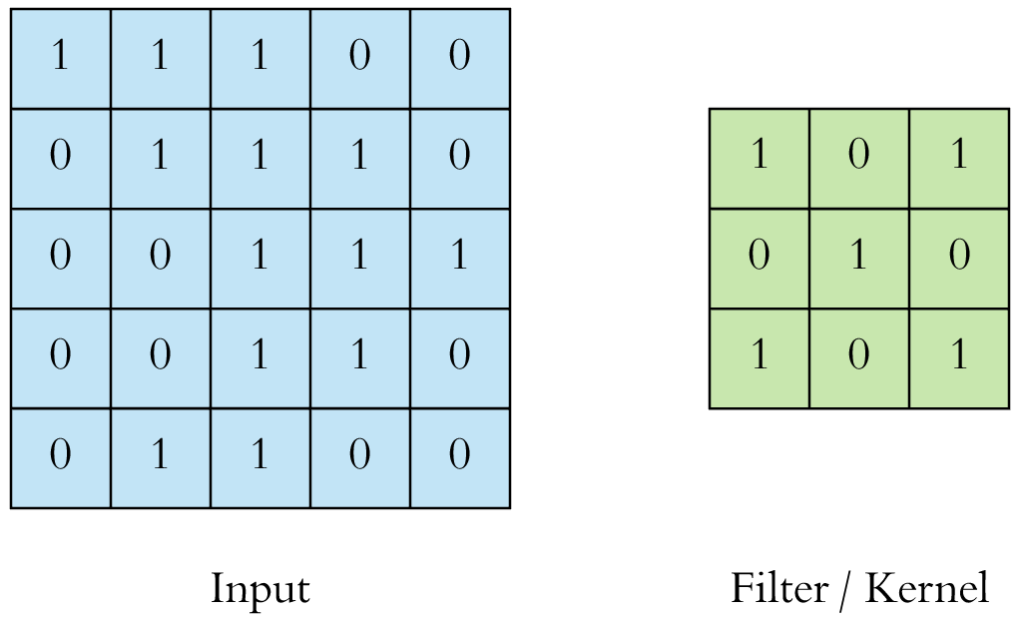
Step 1 – Identify the dimensions of input image together with its values. Below diagram shows a the dimensions of a very small image with pixel values varies between (0 or 1 only). Note in general the values of pixel varies between 0-255

Step 2 – Identification of Kernel (filter) dimensions and its weights.

First part of Kernel (K) is its dimension which remains fixed throughout and defined before we starts with our training. In the below image 3*3 is the dimension of kernel

Second part is Kernel Weights which can have positive, negative, floating values eg. 0.2, -0.5, -1. We also add Kernel Bias to the computation. In general initial kernel Weights + Bias can have any random values, but during training these weights + bias changes for optimization

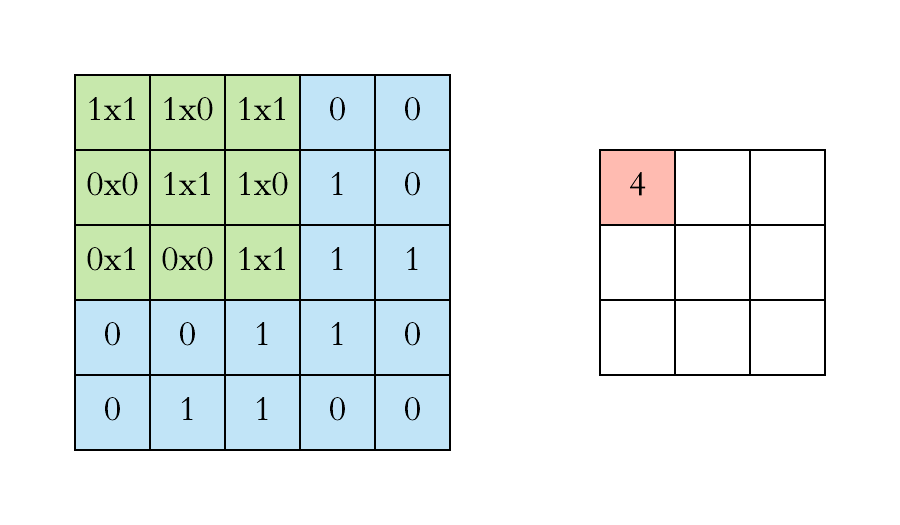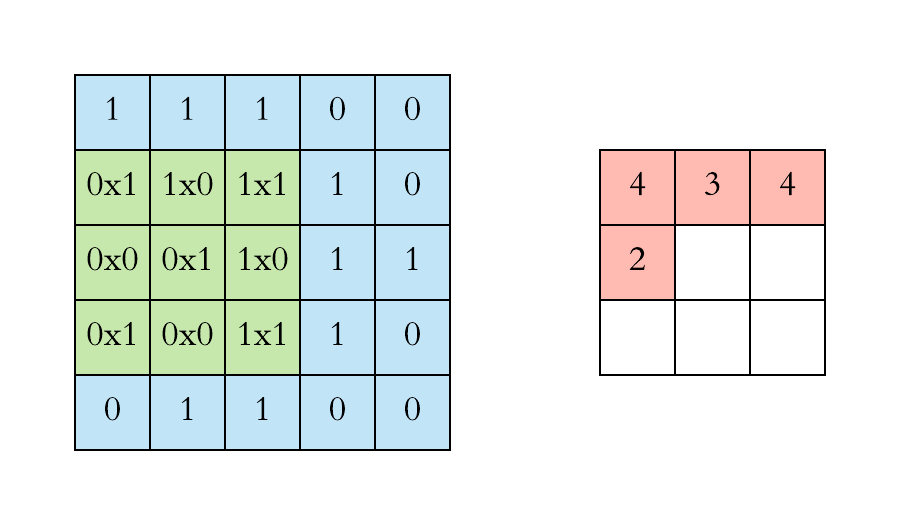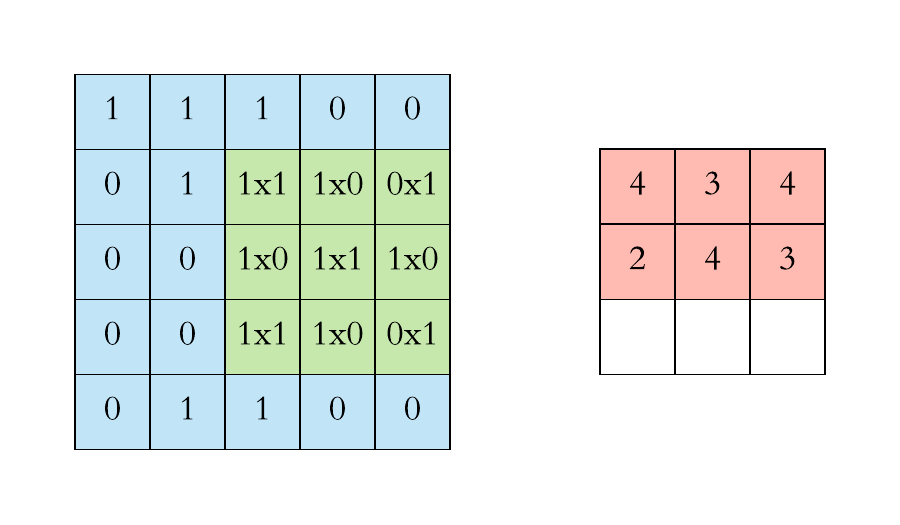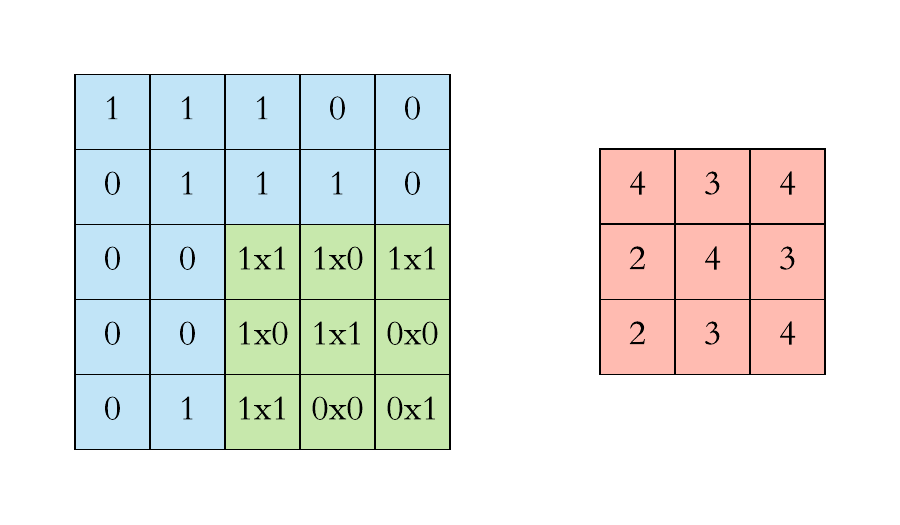
 Output Pixel value = (w1*px1 + w2*px2 + w3*px3 + w4*px4 + w5*px5 + w6*px6) + bias

With this operation all relevant features of the image are identified and a new image with new dimension will be formed for CNN architecture

One important thing to note here is that Convolutions occur per channel. An input image would generally consist of three channels; red, green, and blue. The above example shows convolution operation happening over 2-dimension input image, however actual image is represented in 3-dimensions as Height. Width and Depth where depth is also know as channels which represents the dimension of the image in 3D. 

Now the Kernel is 2-Dimension, so we apply 2 D kernel to all two dimensions of 3-D input image and than all dimensions of input image post kernel operation are merged to get output

Step 3 – Identification of Stride (S) which is a value by which Kernel slides over the input data (pixel by pixel). Default value is 1. In the above GIF Kernel slides by value of 1.

Step 4 – Padding (P) is the amount of default data added to the sides of input image to maintain the size of the output. This is helpful while we slide our kernel over the input image, we don’t end up loosing the data. In the above GIF a layer of zero-value pixels is added to surround the input with zeros, so that we don’t loose features of input image

Let us see the complete picture, here we see Filter count as 2 (as two different Kernels are used), each with a filter size  K = 3 * 3 , stride S = 2, and input padding P = 1

This is very minute level computation happening over input image in CNN architecture.

Bigger Picture on complete image

In CNN architecture we want to optimise the complete image dimensions and parameters while moving across different layers. ( Note at minute level for convolution we will still be doing element-wise matrix multiplication with kernel and sum the result for new value)

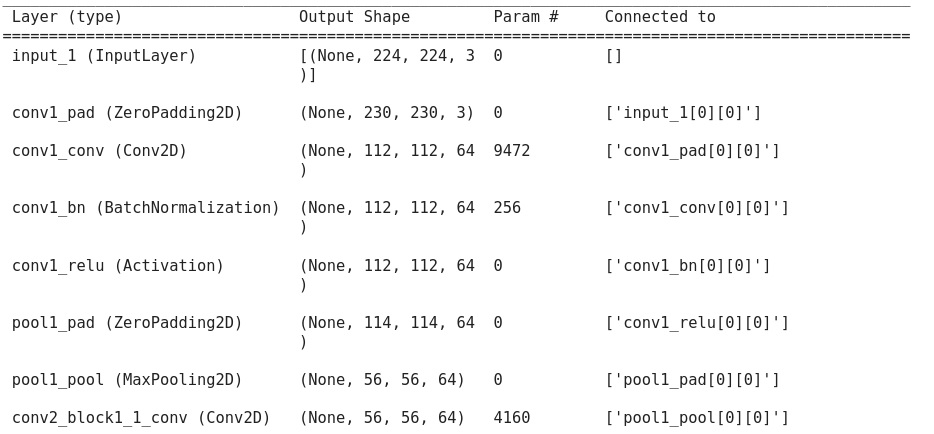
As you you can see in above image input image with dimension of (7*7*3) post convolution gets converted to (3*3*2). Let understand below how the dimensions of complete input image are calculated or changes. Below is screen shot of different dimensions of Resnet50 model:

And the trainable parameters of conv1_conv (convolution layer) would be 9472

Let us do calculations of Output Dimensions in CNN for Convolution Layer

Input Dimensions are defined in format [N H W D]

N : Number of batches or the batch size is the number of 2D images processed together or passes in the ML Model or unique set of weights

H & W : Height and Width of input data ( lets take H=5 and W=5 )

D : Number of depth or the number of features/activation maps

Bias – 1

Output Dimensions are calculated based on below formula

Output (H) = (( Input (H) + 2 P - K )/S) + Bias

Output (W) = (( Input (W) + 2 P - K )/S) + Bias

e.g. -  
Input Dimensions [NHWD] - [None 230 230 3]
Kernel [HWC] - [7 7 64]
Stride [HW] - [2 2]
Padding [H1 H2 W1 W2] - [1 1 1 1]
Bias - 1

Output (H) - ( 230 +2(1) -7)/2 +1 = 112
Output (W) - ( 230 +2(1) -7)/2 +1 = 112
Output (D) - 64
Output (N) - None 

Output dimensions [NHWD] - [ None 112 112 64 ]

Let us do calculation of Output Trainable Parameters

Trainable Parameters – ((Kernel * Kernel * No. of channels) + Bias) X D

e.g. - (( 7 * 7 * 3)+1) * 64 = 9472

The image moves across different layers in Resnet50 model, for current section we are only covering Convolution Layer.